今回の記事ではローレンツ変換の導出を行います。次の相対性原理の記事の続きとして書いているため先にそちらを読むことをお勧めします。
1.ローレンツ変換
1.1.座標変換の係数の検討
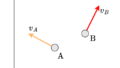
ガリレイ変換のときと同様に、図1のように\(x\)軸方向のみに相対速度\(v\)を持っていると仮定し、ガリレイ変換を一般化して\(\boldsymbol{O’}\)の座標系(\(x’,y’,z’,t’\))を\(\boldsymbol{O}\)の座標系(\(x,y,z,t\))を使って表していきます。\(t=0\)の時2つの座標系は一致しているとします。
図1
まず進行方向に対して垂直な成分の\(y’\)と\(z’\)について考えます。\(y’\)と\(z’\)は同様に考えられるので\(y’\)について見ていきます。空間が等方的で各軸が垂直であり、各軸が勝手に回転しないと仮定すると、\(y’\)軸は\(xz\)平面上に対して垂直になります。この点については詳細に述べている書籍が少なかったためまとめるのに苦労しました。また、\(y’\)が時間\(t\)に依存して変化しているとすると時間の経過により座標系\(\boldsymbol{O’}\)が\(y\)方向に移動していることになり、\(x\)軸方向以外に速度を持つことになり最初の仮定に反します。以上により、\(y’\)は相対速度\(v\)に依存した係数\(a\)に比例することになります(式(1))。
$$y’=ay \tag{1}$$
\(\boldsymbol{O}\)の座標系(\(x’,y’,z’,t’\))を\(\boldsymbol{O’}\)の座標系(\(x,y,z,t\))を使って表そうとした場合も同じことがいえるため式(9)が得られます。
$$y=ay’ \tag{2}$$
式(1)を式(2)に代入すると、
$$a^2=1 \tag{3}$$
となります。\(a=-1\)とすると式(1)が
$$y=-y’ \tag{4}$$
となり\(y\)軸が反転することになるため\(a=1\)となります。\(z\)軸も同様に考えて次の式が得られます。
$$y’=y \tag{5}$$
$$z’=z \tag{6}$$
次に進行方向である\(x’\)について考えます。\(\boldsymbol{O’}\)の原点は\(t\)秒経過後には\(vt\)の位置にあるので、ガリレイ変換と同じ\(x-vt\)という形が出てくると考えられます。これに相対速度\(v\)に依存した係数\(b_1\)をかけた形で表せます。\(b_2\)と\(b_3\)も\(y\)、\(z)に関する同様な係数とします。
$$x’=b_1(x-vt)+b_2y+b_3 z \tag{7}$$
\(x=0\)、\(t=0\)の時、\(x’=0\)となるため\(b_2=b_3=0\)となり、\(b_1=b\)として式(8)が得られます。
$$x’=b(x-vt) \tag{8}$$
最後に時間について次のような変換をします。
$$t’=d_1 x+d_2 y+d_3 z+d_4 t \tag{9}$$
ここまでをまとめると、以下の4式が座標変換を表す式になり、その係数をこれから決めていきます。
$$x’=b(x-vt) \tag{10}$$
$$y’=y \tag{11}$$
$$z’=z \tag{12}$$
$$t’=d_1 x+d_2 y+d_3 z+d_4 t \tag{13}$$
1.2.光速度不変の原理
ここで光速度不変の原理を使います。図2の上の図のように、\(t=t’=0\)では2つの座標系は一致していて、この瞬間にそれぞれの座標系の原点から光が発せられたとします。\(\boldsymbol{O}\)座標から見た場合は静止しているため原点\(O\)を中心に同心円状に広がっていきます。\(t\)秒後のその半径は\(ct\)です。\(c\)は光速を表しています。
図2
この球は式(14)で表されます。
$$x^2+y^2+z^2=(ct)^2 \tag{14}$$
\(\boldsymbol{O’}\)座標から見た場合も同様に考えられ、原点\(O’\)を中心に同心円状に広がっているように見えるはずです。相対速度\(v\)で移動してるため時間の流れが\(\boldsymbol{O}\)座標と異なり\(t’\)となるため、球の半径は\(ct’\)となります。光速はどちらの座標系でも\(c\)であり、この球を表したのが式(15)です。
$$x’^2+y’^2+z’^2=(ct’)^2 \tag{15}$$
式(15)に座標変換式(10)~(13)を代入して式(14)と一致すれば光速度不変の原理を満たす座標変換が得られ、係数を決めることでローレンツ変換を求めます。係数が多いため少しずつ減らしながら計算していきます。上述のように式(15)に式(10)~(13)を代入します。
$$b^2(x-vt)^2+y^2+z^2=c^2(d_1 x+d_2 y+d_3 z+d_4 t)^2 \tag{16}$$
この計算をする上で、\(xy\)、\(xz\)、\(yz\)、\(yt\)、\(zt\)の項は式(14)と比較した際にも1つしか出てこないためその係数は0になります。\(d_2=d_3=0\)とすることで上記の項を消去できます。
$$b^2(x-vt)^2+y^2+z^2=c^2(d_1 x+d_4 t)^2 \tag{17}$$
これを解いて整理すると式(18)になります。
$$(b^2-c^2d_1^2)x^2+y^2+z^2=(c^2d_4^2-v^2b^2)t^2+2(vb^2+c^2d_1 d_4)xt \tag{18}$$
これを式(14)と比較すると次の3式が得られます。ここまでで残っている未知の係数は\(b\)、\(d_1\)、\(d_4\)です。
$$b^2-c^2d_1^2=1 \tag{19}$$
$$c^2d_4^2-v^2b^2=c^2 \tag{20}$$
$$vb^2+c^2d_1 d_4=0 \tag{21}$$
式(19)を移項して、
$$b^2=c^2d_1^2+1 \tag{22}$$
式(22)を式(20)、(21)に代入
$$c^2d_4^2=c^2+c^2v^2d_1^2+v^2 \tag{23}$$
$$c^2d_1 d_4=-(vc^2d_1^2+v) \tag{24}$$
式(24)を二乗して式(23)を代入後整理すると式(25)が得られます。
$$d_1^2=\frac{v^2}{c^2}\frac{1}{c^2-v^2} \tag{25}$$
式(25)を式(23)に代入して整理すると式(26)が得られます。
$$d_4^2=\frac{1}{1-\frac{v^2}{c^2}} \tag{26}$$
次に式(25)を式(22)に代入すると、式(27)が得られます
$$b^2=\frac{1}{1-\frac{v^2}{c^2}} \tag{27}$$
\(v=0\)の時2つの座標系は一致するため、変換式(10)
$$x’=b(x-vt) \tag{10}$$
に\(v=0\)を代入すると\(b\)は正であることがわかります。式(27)より\(b\)が求まります。
$$b=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}} \tag{28}$$
ここで変換式(13)に戻って係数を整理すると式(29)となります。
$$t’=d_1 x+d_4 t \tag{29}$$
また、\(v=0\)の時\(d_1=0\)となるため、2つの座標系が一致するためには\(d_4\)も正である必要があります。よって式(26)より\(d_4\)が求まります。
$$d_4=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}} \tag{30}$$
最後に、式(28)、式(30)を式(21)に代入することで\(d_1\)が求まります。
$$d_1=-\frac{\frac{v}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}} \tag{31}$$
求まった係数式(28)、(30)、(31)を式(10)、(29)に代入すると座標変換の式(32)、(33)が求まる。
$$t’=\frac{t-\frac{vx}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}} \tag{32}$$
$$x’=\frac{x-vt}{\sqrt{1-\frac{v^2}{c^2}}} \tag{33}$$
ここで、時間に光速\(c\)をかけて距離の単位となる\(\omega=ct\)、\(\omega’=ct’\)という形を用いて次の式変形を行います。
$$ct’=\omega’=c\frac{t-\frac{vx}{c^2}}{\sqrt{1-\frac{v^2}{c^2}}}=\frac{\omega-\frac{v}{c}x}{\sqrt{1-\frac{v^2}{c^2}}} \tag{34}$$
$$x’=\frac{x-vt}{\sqrt{1-\frac{v^2}{c^2}}}=\frac{x-\frac{v}{c}\omega}{\sqrt{1-\frac{v^2}{c^2}}} \tag{35}$$
また、式の中に出てきている形を次の文字で置き換えます。\(\beta\)は光速に対する相対速度\(v\)を表し、\(\gamma\)はローレンツ係数と呼ばれます。
$$\beta=v/c \tag{36}$$
$$\gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}} \tag{37}$$
式(34)、(35)を式(36)、(37)を用いて表しなおすと式(38)、(39)が得られます。
$$\omega’=\gamma(\omega-\beta x) \tag{38}$$
$$x’=\gamma(x-\beta \omega) \tag{39}$$
これでローレンツ変換が導かれました。時間と距離が\(\beta\)、\(\gamma\)を用いることで対称性を持った形で表すことができます。\(\boldsymbol{O’}\)座標の\(x’\)と\(t’\)は\(\boldsymbol{O}\)の位置\(x\)と時間\(t\)を用いて表され、位置の変換に時間が、時間の変換に位置が含まれており、相対的に速度を持つことで時間と空間が影響しあっていることがわかります。
ここで、座標返還式(32)、(33)において相対速度\(v\)が光速\(c\)に対して非常に小さいと仮定すると\(v/c≒0\)となりガリレイ変換と一致します。
$$t’=t \tag{40}$$
$$x’=x-vt \tag{41}$$
私たち人間が日常で体感できる範囲の世界では光速に近づくような現象はないため、ガリレイ変換で問題なく座標変換を行うことがわかります。
今回はアインシュタインが使った原理を用いて導出しましたが他にもマクスウェル方程式を不変に保つようにして導出する方法があります。他にも方法があるみたいですが機会があれば調べてみたいと思います。今回の記事は以上になります。
参考文献
1.中野董夫、相対性理論、岩波書店、2021
2.広江克彦、趣味で相対論、理工図書株式会社、2019


コメント