【高校物理：力学】基本的な物理量(位置・速度・加速度)

図1

　図1のように\(xy\)座標で、\(x\)軸上の任意の位置に物体Aが存在しているとします。物体Aの\(x\)軸方向の位置は\(x\)軸上の数値として表せるのでその位置を\(x\)[m]と表します。\(x\)軸上の4[m]の位置にあるとすると\(x\)=4[m]となります。\(x\)軸方向だけでなく\(y\)軸方向も同じ事が言えます。平面ではなく3次元空間の位置を表すと\(z\)軸が必要になりますが3次元空間は高校物理では多分出てこないです。\(xz\)座標で考える問題はよく出てきます。また、位置を表す記号として\(\boldsymbol{r}\)もよく使われます。半径(radius)を表す時にも使われます。

1.2 速度

　速度は単位時間当たりに進む距離のことです。\(\boldsymbol{v}\)(velocityの頭文字)を使って表します。由来はよくわかりませんが\(\boldsymbol{u}\)もよく使われます。物理では時速ではなく、1秒間当たりに何m進むかを表す秒速で考えるので単位は[m/s]になります。sは秒(second)です。単位の[m/s]は距離/時間を表しています。距離を時間で割っています。これを式にすると式(2)になります。\(\Delta\)はその物理量がどれだけ変化したかを意味しています。

$$v=\frac{\Delta x}{\Delta t}\tag{2}$$

　車が一定の速度で20[m](\(\Delta x\))進むのに2[s](\(\Delta t\))かかったとすると、1[s]で10[m]進むことができます。これが速度\(v\)で10[m/s]と表します。身近な概念なのでイメージはしやすいと思います。式(1)では「速さ」となっていますが、「速度」とは意味が異なります。これについては後述します。

1.3 加速度

　続いて加速度です。これは高校物理で初めて聞く言葉ではないかと思います。加速度は単位時間当たりに速度がどれだけ変化したかを表し、\(\boldsymbol{a}\)(acceleration)とか\(\boldsymbol{\alpha}\)がよく使われます。単位は[m/s\(^\mathrm{2}\)]です。メートル毎秒毎秒と読みます。初めて見る時はよくわからないと思うので、[(m/s)/s]と考えるとわかりやすいと思っています。これは速度/時間を表していて速度を時間で割っています。これは式(3)で表せます。

$$a=\frac{\Delta v}{\Delta t}\tag{3}$$

　身近な例では駅で止まっている電車が動き出してある速度に達するまでの動きがわかりやすいです。速度0[m/s]で静止していた電車が速度100[m/s]まで一定の加速度で加速したとします(\(\Delta v=100[\mathrm{m/s}]\))。この速度になるまでに10[s](\(\Delta t\))かかったとしたら加速度\(a\)は10[m/s\(^\mathrm{2}\)]で、1[s]に10[m/s]ずつ速度が大きくなり10[s]後に100[m/s]になります。

2.物理量の大きさと向き

　位置、速度、加速度の3つの物理量は大きさだけではなく向きも持っています。大きさと向きを持つものをベクトルといいます。そのため3つの物理量はベクトルになります。大きさしか持たない場合はスカラーです。時間はスカラーです。この2つは初めて勉強する時はよくわからないと思いますが少しずつ慣れていけばいいと思います。

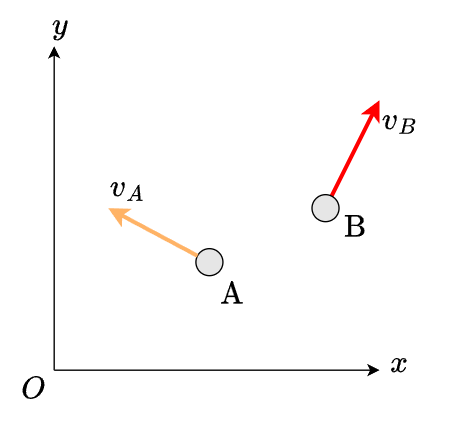
　ベクトルについては別に記事を書こうと思いますが、速度ベクトルを例に簡単に説明します。図2の物体Aと物体Bがそれぞれ速度\(\boldsymbol{v_A}\)と\(\boldsymbol{v_B}\)で運動していて、どちらも10[m/s]であるとします。同じ10[m/s]ですがAは左上に、Bは右上に進んでいて向きは異なっています。右上に10[m/s]で進んでいるという数量の大きさだけでなく向きを持った量を速度と言います。速度はベクトルです。また、速さは10[m/s]という速度の大きさのことを言います。このようにベクトルの大きさもスカラーです。今回の例では運動の向きが違うので速度は異なりますが、どちらも同じ10[m/s]で進んでいるので速さは同じです。

図2

　このことは加速度についても同じことが言えます。加速度がベクトルでその大きさを加速度の大きさと言います。速さは速(度の大き)さではないです。

　最後に位置ベクトルについてです。図3に点Aと点Bがあり、どちらも原点Oからの距離は等しくその大きさを\(r\)とします。点Oから点A、点Bへの位置ベクトルはそれぞれ\(\boldsymbol{r_A}\)、\(\boldsymbol{r_B}\)とすると式(4)のように表せます。

$$|\boldsymbol{r_A}|=|\boldsymbol{r_B}|\tag{4}$$

　OAとOBの距離は等しいので位置ベクトル\(\boldsymbol{r_A}\)と\(\boldsymbol{r_B}\)の大きさが同じになります。しかし、図の通り点Oから見て点Aと点Bがある向きは異なっています。位置ベクトルの向きは異なっているということです。大きさは同じでも向きが異なるとその物理量のベクトルは違うことを意味していることになります。整理すると、位置はベクトルを表し、位置ベクトルの大きさのことを距離と言います。距離はその大きさのみで決まるもので、どの方向を向いているかは関係ありません。点Aを向いていても点Bを向いていても、その距離が100[m]であればその値は変わりません。位置の他にも長さ\(L\)または\(l\)(Length)や高さ\(H\)または\(h\)(Height)もよく使われます。場面によって他にも違う文字が使われます。上述した\(\boldsymbol{x}\)と\(\boldsymbol{y}\)については、数直線上の座標として正か負のどちらかの方向を向いた1次元ベクトルになります。色んな文字が出てきていますが何度も出てきてそのうち覚えてくるので今覚えようとする必要はないです。高さ\(\boldsymbol{h}\)も鉛直方向の運動について1次元ベクトルとして考えることもできるようです。

図3

　ここからは余談で私の想像が混ざりますが、位置を表す文字として\(r\)が使われるのは太陽等の天体の運動について考えられていたからだと思います。天文学では古くから地球を中心に回転する太陽等の天体の軌道が計算されていました。このような回転運動では位置として半径\(r\)が使われます。天文学で位置を表していた半径\(r\)がそのまま他の運動にも使われたのかと思います。

3.最後に

　高校物理では微積を使わないで解くことになっていますが、大学以降で物理学は微積を使って表します。微積はニュートン(とライプニッツ)が考案したもので、力学の運動を記述するために必要だったので生まれたと言われています。今回説明した物理量についても、位置を微分すると速度、速度を微分すると加速度になり、物理と微積は切り離せないものです。趣味として物理を楽しむには微積を使って理解できるとより楽しめると思っています。そのうち微積を使った記事も書きたいと思っています。

　ハイレベルな受験生は微積を使って解くように予備校で指導されたり微積物理の参考書を使うこともありますが、前述のとおり高校物理では微積は使わないことになっているので無理にやる必要はないです。余裕と興味がない人は手を出す必要はないです。私が受験生の頃は物理で微積を使う事自体知らなかったです。

3.1.例題

　最後に例題を出して終わります。今回はグラフの説明をしていないのでわからなければ次回の記事を読んでから解いてみてください。次回の記事の最後に解説します。

　時刻\(t\)=0[s]で静止していた電車が1.5[m/s\(^\mathrm{2}\)]の加速度で動き出し、20[s]の間一定の加速度で運動した。120[s]一定速度で進んだ後、-1[m/s\(^\mathrm{2}\)]の加速度で運動を続けて静止した。静止した時刻\(t_1\)を求め、この運動について加速度\(\boldsymbol{a}\)と時間\(t\)の関係(\(\boldsymbol{a}\)-\(t\)グラフ)、速度\(\boldsymbol{v}\)と時間\(t\)の関係(\(\boldsymbol{v}\)-\(t\)グラフ)をそれぞれグラフに表せ。加速度\(\boldsymbol{a}\)と速度\(\boldsymbol{v}\)を縦軸とし、時間\(t\)を横軸とする。

　次回は等加速度運動について、今回説明した物理量の関係を表す数式についてまとめます。今回の記事は以上になります。

【高校物理：力学】等加速度運動の基本公式(+ジャーク)

今回は等加速度運動の基本的な式についてまとめます。この記事で使用する物理量についてはこちらの記事にまとめています。1.等加速度運動　等加速度運動はその名前の通り加速度が一定の時の運動のことです。一定の加速度で速度が変化することになります。初...

butsuriblog.com

2025.04.28

　参考文献
1.浜島清利、物理のエッセンス 五訂版、河合出版、2023