力学の基本の力のつりあいと、重力と垂直抗力を取り上げます。
この記事は素人が理解を整理するためにまとめたものです。考え方の1つとして参考になれば幸いです。前回の記事はこちら。
力学の記事一覧と体系図。
1.力のつりあい
ある物体に複数の力がはたらいていて、その物体の運動の状態が変化しない時、物体は力がつりあっているといいます。簡単な例として綱引きについて考えてみます(図1)。
図1
これは綱だけに注目した図で、両者の力が拮抗していて動いていない状態です。これが力のつりあいです。この状態から仮に右側の力が大きくなると、力がつり合わなくなって右向きに動きだします。この例は静止している時の話ですが、動いていても同じです。一定速度で移動している物体にはたらく力がつりあっていれば物体は速度を変えず移動し続けます。これが前述した運動の状態が変化しないということです。静止している物体は静止し続け、移動している物体は同じ速度で移動し続けます。中学の理科でも出てきたかと思います。
ここで、物体を移動させ続けるには力を与え続ける必要があると直感的に感じるかもしれません。前回も同じ話をしましたが改めて説明します。実際に重いものを移動させるには押し続ける必要があります。これは図2のように表せます。
図2
図2のような場合では摩擦力が発生していて、物体の運動を妨げようとする力がはたらいています。摩擦力と同じ力で押すことで力がつりあい、この状態が変化しなければ一定速で進み続けることができます(静止している状態から動かすためには摩擦力より大きい力で押すことが必要です)。もし摩擦力が無ければ、力を与えない限りその状態が維持されます。物体を移動させ続けるために力は必要というわけではないことになりますね。
2.重力
2.1.重力について
重力は身近な力の1つだと思います。重力は天体のような大きな物体に引っ張られる力です。実際には全ての物体から互いに引き合う力(万有引力)を受けていますが、地球のような非常に大きい物体(質量)でないとその力を感じられないほど小さいです。物体の質量を\(m\)、重力加速度を\(g\)とすると重力は\(mg\)と表せます。重力は天体によって異なりますが、問題文に書いてなければ地球の話です。地球の重力加速度\(g\)も緯度や地球の中心からの距離でも少し変わります。緯度で変わるのは自転による遠心力があるためです。場所によって一定ではないですが、高校物理では地上での重力加速度は9.8[m/s\(^2\)]とすることが多いです。赤道上は遠心力が最大になるため重力が最も小さくなり、遠心力が小さい北極や南極では重力が大きくなります。また、自転により地球は厳密には球ではなく、赤道は半径が最も大きく中心から遠いことも重力が小さい理由です(参考文献2)。
重力に関して、質量が大きい物体(重い物体)と質量が小さい物体(軽い物体)の落下について考えてみます。どちらの物体が速く落下するでしょうか。重い物体を10[kg]の鉄球、軽い物体を0.001[kg]の羽としてそれぞれの質量を\(M\)、\(m\)とします。直感的には羽の方がゆっくり落ちるイメージがあると思います。ガリレオはどちらも同じ速度で落下すると考えてピサの斜塔でこの実験をしたそうです(作り話という説もあります)。重力だけがはたらいていると仮定して、運動方程式からそれぞれの加速度\(a_1\)、\(a_2\)を求めてみます。
鉄球
$$\begin{align}M\boldsymbol{a_1}&=Mg\\
\boldsymbol{a_1}&=g\tag{1}\end{align}$$
羽
$$\begin{align}m\boldsymbol{a_2}&=mg\\
\boldsymbol{a_2}&=g\tag{2}\end{align}$$
どちらも加速度は重力加速度と等しくなります。前回も触れましたが質量は動きにくさを表します。重い鉄球にはたらく重力は羽より大きいですが、重い分動きにくくなります。鉄球を動かすためには大きな力が必要ということです。羽はその逆で、重力は小さいですが軽い分小さい力で動かせます。式変形を見てもわかる通り、両辺に物体の質量が出てくるため質量に関係なく落下の加速度は重力加速度と等しくなります。では何故羽の方がゆっくり落ちるイメージがあるのかというと、重力と逆方向に空気抵抗がはたらくためです。空気抵抗は物体のはやさや大きさ等により大きさが決まり、同じ形状の場合質量によらず同じ大きさになります。そのため軽い羽の方が重力に対する空気抵抗の影響が大きくなり、羽の落下速度が小さくなります。空気抵抗がない場合は上で計算した通りです。この条件の実験を、NASAがアポロ15号で月に行った時に行っています。ハンマーと羽を落下させる動画がNASAの公式サイトにあるのでリンクを貼っておきます。
The Apollo 15 Hammer-Feather Drop – NASA Science(NASA公式サイト)
動画を見てみるとハンマーと羽が同時に落下しています。月には大気がなくほぼ真空で空気抵抗がないためです。これによりガリレオの主張が正しいことが確かめられました。また、重力加速度は天体によって異なり、月では地球の1/6程になります。動画の実験でもゆっくり落下していますね。
2.2.重力と質量の違い
質量と重力という言葉が出てきましたが、その違いはわかるでしょうか。基本的な事ですが大事なので確認しておきます。曖昧な人は一度考えてみてください。
質量は物体が持っている物理量で、その値は場所によって変わることはありません。それに対して重力は質量と重力加速度の積です。そのため、物体がどこに存在しているかで変わります。前述の通り月の重力加速度は地球の1/6です。質量は地球でも月でも同じですが、月の重力は地球の1/6となります。質量はどこでも同じで、重力はその質量が存在する位置における重力加速度によって変わる物理量であるということです。
3.垂直抗力
次に垂直抗力についてです。地面に置かれている物体は重力を受けています。物体が地上で静止していられるのは地面が物体を押し返しているためです。この地面が物体を押し返す力を垂直抗力(Normal Force)と言い、\(\boldsymbol{N}\)で表されます。Normalには「垂直な」という意味もあるようです。床に置いた物体の力のつりあいを見てみます(図3)。
図3
物体の重心\(G\)から下向きに重力\(mg\)、床との接点(重力と同じ作用線上の点)から上向きに垂直抗力\(\boldsymbol{N}\)がはたらきます。静止しているため力のつりあいから垂直抗力\(\boldsymbol{N}\)は重力\(mg\)と等しくなります。
$$\boldsymbol{N}=mg\tag{3}$$
図に力を書くときはこのように力が始まる点(作用点)から矢印を書きます。向きがわからない場合はどちらかの方向を仮定して解きます。仮定した向きと逆だと計算結果が負になるのでそこで最初の仮定が逆だったとわかります。問題を解いてるとわかってくると思います。
次に、上向きの力\(\boldsymbol{F}\)(\(\boldsymbol{F}<mg\))が物体にはたらいた場合を見てみます(図4)。
図4
上向きに力\(\boldsymbol{F}\)がはたらいていますが、重力より小さいため静止したままになります。力のつりあいから式(4)が得られ、\(\boldsymbol{N}\)が求まります(式5)。
$$\boldsymbol{F}+\boldsymbol{N}=mg\tag{4}$$
$$\boldsymbol{N}=mg-\boldsymbol{F}\tag{5}$$
\(\boldsymbol{F}\)がはたらいている分式(3)と比べて\(\boldsymbol{N}\)が小さくなっています。\(\boldsymbol{F}\)を大きくしていき、重力と等しくなると\(\boldsymbol{N}\)は0に浮き上がる直前の状態になります。空中で\(\boldsymbol{F}\)と重力がつりあってるのと同じような状態です。この時点で垂直抗力\(\boldsymbol{N}\)はなくなり、\(\boldsymbol{F}\)が重力より大きくなっても式(5)で\(\boldsymbol{N}\)が負になるようなことはありません。ちなみに地面は作用反作用の法則により、物体から\(\boldsymbol{N}\)と同じ大きさで下向きの力を受けています。
4.例題
4.1.前回の例題
問題
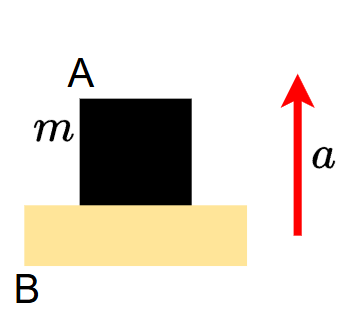
図5のように物体Bが鉛直方向に加速し、物体Aと一体になって等加速度運動をしている。上向きを正とし、加速度の大きさを\(a\)、重力加速度の大きさを\(g\)、物体Aの質量を\(m\)とする。
(1).加速度が上向きの場合に物体Aが受ける垂直抗力\(N_1\)を求めよ。
(2).加速度が下向きの場合に物体Aが受ける垂直抗力\(N_2\)を求めよ。
図5
解説
前回の記事で出していた例題の解説です。この問題はエレベーターに乗っている時に感じる力がこの問題の状況に当てはまります。今回は地上(エレベーターの外)からの視点で考えます。
(1).上向きを正とした物体Aの運動方程式より式(E-1)が得られ、式(E-2)のように\(N_1\)が求まります。
$$N_1-mg=ma \tag{E-1}$$
$$N_1=m(g+a) \tag{E-2}$$
重力に逆らって上向きに加速度が生じているため、加速度がかかった分静止している時と比べて物体Aにかかる重力より垂直抗力が大きくなっています。加速度が0だと重力と一致します。
(2).下向きに加速度が生じている場合加速度は\(-a\)です。先程とは逆に重力に対して垂直抗力が小さいことになります。運動方程式から同様にして式(E-3)が求まります。
$$N_2-mg=m(-a)$$
$$N_2=m(g-a) \tag{E-3}$$
重力方向に物体を降ろすように加速度が生じているため、物体Aにかかる重力から加速度がかかった分垂直抗力が小さくなっています。
このように加速度が生じることで物体Aが床から受ける垂直抗力が変わってきます。これはエレベーターに乗っている時に身近に起きている現象です。具体的な数字で見てみます。100[kg]の人が乗っているエレベーターが1[m/s\(^2\)](参考文献3の乗り心地に関する研究で使われている値から仮定)で昇降した時の\(N_1\)と\(N_2\)を求めてみます。また比較のために静止している時の垂直抗力\(N\)も計算しておきます。計算を簡単にするために重力加速度は10[m/s\(^2\)]とします。
$$N=mg=1,000[\mathrm{N}] \tag{E-4}$$
$$N_1=m(g+a)=1,100[\mathrm{N}] \tag{E-5}$$
$$N_2=m(g-a)=900[\mathrm{N}]\tag{E-6}$$
今回はエレベーターの加速度が重力加速度の±10%となっていて、加速度の影響を受けて垂直抗力も同様に±10%増減しています。登り始めと降り始めで重く感じたり軽く感じるのはこのためです。垂直抗力は重力と一定というわけではないことがわかります。また、物体Bが物体Aから受ける力の大きさは作用反作用の法則より物体Aの垂直抗力と同じです。
余談です。高校物理とは関係ないです。力の単位としてkgf(キログラムフォース、キログラム重)というものがあります。1[kgf]=9.8[N](単位の定義なのでここだけ問題とは別に\(g\)を正確な値にしています)の関係があります。力を重力加速度で割るとこの[kgf]の大きさになり、力を見かけ上質量と同じ数値で表示できます。質量と同じ感覚で直感的に考えられるので工学系でよく出てきます。他の分野ではわかりません。式(E-4)~(E-6)をこの単位にしてみます。計算結果をわかりやすくするために1[kgf]≒10[N]とします。
$$N=1,000[\mathrm{N}]=100[\mathrm{kgf}] \tag{E-4′}$$
$$N_1=1,100[\mathrm{N}]=110[\mathrm{kgf}] \tag{E-5′}$$
$$N_2=900[\mathrm{N}]=90[\mathrm{kgf}]\tag{E-6′}$$
100[kg]の人が静止していると重力は100[kgf]になります。そのまんまですね。エレベーターに置いた体重計に乗って昇降するとそれぞれ110[kg]と90[kg]になります。体重計の数字は[kgf]に相当するので。[kgf]で考えるとイメージしやすいかも?そういう単位もあるという紹介でした。
次回は力の分解と合成についてです。
1.浜島清利、物理のエッセンス 五訂版、河合出版、2023
2.国立天文台、暦Wiki 天体の形状、https://eco.mtk.nao.ac.jp/koyomi/wiki/C5B7C2CEA4CEB7C1BEF5.html (最終閲覧日:2026年2月9日)
3.上條 芳武、岩田 宜之、高田 一、エレベータの乗り心地に影響するパラメータの推定、https://www.jstage.jst.go.jp/article/transjsme/86/881/86_19-00407/_pdf、日本機械学会論文集、2020
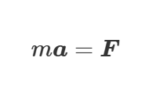
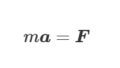
コメント