1.はじめに
私たちの身の回りには電磁波がたくさん存在しています。ラジオに使われる電波や病院の検査で使われるX線、人が見ることができる光(可視光)も電磁波の一種です。この記事ではそんな電磁波の導出についてまとめました。
電磁波を導くためにはマクスウェル方程式を使います。マクスウェル方程式を式変形していくと波動方程式が現れ、その波動方程式が電磁波を表します。マクスウェル方程式と波動方程式については過去にまとめているので、これらの式について知らない方はそちらを先に読んでいただくと理解の助けになるかもしれません。
2.電磁波の導出
初めにマクスウェル方程式を示しておきます。太陽や星の光が宇宙空間から地球に届いて人間が見ることができるように、電磁波は何もない真空中を進むことができることになります。何もない空間を伝わるという条件のために式(1)右辺の電荷密度\(\rho\)と式(3)右辺の電流密度\(i\)を0となるように書き直します。
$$\mathrm{div}{\boldsymbol{E}}=0 \tag{1}$$$$\mathrm{div}{\boldsymbol{B}}=0 \tag{2}$$$$\mathrm{rot}{\boldsymbol{H}}-\frac{\partial \boldsymbol{D}}{\partial t}=0 \tag{3}$$$$\mathrm{rot}{\boldsymbol{E}}+\frac{\partial \boldsymbol{B}}{\partial t}=0 \tag{4}$$
式(4)の両辺に\(\mathrm{rot}\)をかけて
$$\mathrm{rot}\,\mathrm{rot}{\boldsymbol{E}}+\mathrm{rot}\frac{\partial \boldsymbol{B}}{\partial t}=0 \tag{5}$$
ここで式(6)を用います。次の記事を参考にしてください。下の計算で出てくるラプラシアンについてもまとめています。
$$\mathrm{rot}\,\mathrm{rot}\boldsymbol{A}=\mathrm{grad}\,\mathrm{div}\boldsymbol{A}-\mathrm{div}\,\mathrm{grad}\boldsymbol{A} \tag{6}$$
式(6)を式(5)に代入します。
$$\mathrm{grad}\,\mathrm{div}\boldsymbol{E}-\mathrm{div}\,\mathrm{grad}\boldsymbol{E}+\mathrm{rot}\frac{\partial \boldsymbol{B}}{\partial t}=0 \tag{7}$$
式(1)より式(7)の第一項は0になるため。
$$-\mathrm{div}\,\mathrm{grad}\boldsymbol{E}+\frac{\partial }{\partial t}\mathrm{rot}\boldsymbol{B}=0 \tag{8}$$
$$-\bigtriangleup\boldsymbol{E}+\mu_0\frac{\partial }{\partial t}\mathrm{rot}\boldsymbol{H}=0 \tag{9}$$
式(3)を代入します。
$$-\bigtriangleup\boldsymbol{E}+\mu_0\frac{\partial^2}{\partial t^2}\boldsymbol{D}=0 \tag{10}$$
$$-\bigtriangleup\boldsymbol{E}+\mu_0\varepsilon_0\frac{\partial^2}{\partial t^2}\boldsymbol{E}=0 \tag{11}$$
$$(\bigtriangleup-\mu_0\varepsilon_0\frac{\partial^2}{\partial t^2})\boldsymbol{E}=0 \tag{12}$$
式(12)が電磁波を表す波動方程式です。これを次のように変形すると参考記事と似た形の方程式が得られます。参考記事では1次元でしたが、次式は3次元の波動方程式で電磁波を表しています。
$$\bigtriangleup\boldsymbol{E}=\mu_0\varepsilon_0\frac{\partial^2 \boldsymbol{E}}{\partial t^2} \tag{13}$$
$$\frac{\partial^2 \boldsymbol{E}}{\partial t^2}=\frac{1}{\mu_0\varepsilon_0}(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2})\boldsymbol{E} \tag{14}$$
ここで\(\mu_0\)は真空の透磁率、\(\varepsilon_0\)は真空の誘電率であり、これらの値は定数です。
$$\mu_0=4\pi×10^{-7}\,[\mathrm{N}/\mathrm{A}^2] \tag{15}$$
$$\varepsilon_0=8.854×10^{-12}\,[\mathrm{A}^2\mathrm{s}^2/\mathrm{N}\mathrm{m}^2] \tag{16}$$
波動方程式の性質から
$$\frac{1}{\sqrt{\mu_0\varepsilon_0}}=c_0$$
が電磁波が伝わる速度になり、この速度は真空中を伝わる光の速度\(c_0\)と一致します。
$$c_0=2.998×10^8\,[\mathrm{m}/\mathrm{s}] \tag{15}$$
このことが光が電磁波であるという根拠の一つとなりました。
ここまでは電場についての式でしたが、式(3)に\(\mathrm{rot}\)をかけて同様に計算することで磁場についても同様の式を導くことができます。
$$(\bigtriangleup-c_0\frac{\partial^2}{\partial t^2})\boldsymbol{B}=0 \tag{16}$$
3.電磁波の伝わり方
マクスウェル方程式の式(3),(4)において電場と磁場が影響しあうことで、式(12),(16)で表される電磁波が生じました。この電磁波がどのように伝わっているかを見ていきます。ここでは1次元の波動関数として考えるために、\(x\)軸方向に対してのみ値が変化するように電場\(\boldsymbol E\)と磁場\(\boldsymbol B\)が\(x\)と\(t\)の関数であると仮定します。\(y\)方向と\(z\)方向に移動しても値が変化しないことになります。ここで\(\boldsymbol E\)と\(\boldsymbol B\)を次のように定義します。
$$\boldsymbol E=(E_{x}(x,t), E_{y}(x,t), E_{z}(x,t)) \tag{17}$$
$$\boldsymbol B=(B_{x}(x,t), B_{y}(x,t), B_{z}(x,t)) \tag{18}$$
また、この後の計算でマクスウェル方程式を使うので再掲しておきます。
$$\mathrm{div}{\boldsymbol{E}}=0 \tag{1}$$$$\mathrm{div}{\boldsymbol{B}}=0 \tag{2}$$$$\mathrm{rot}{\boldsymbol{H}}-\frac{\partial \boldsymbol{D}}{\partial t}=0 \tag{3}$$$$\mathrm{rot}{\boldsymbol{E}}+\frac{\partial \boldsymbol{B}}{\partial t}=0 \tag{4}$$
式(4)に式(17)、(18)で表される電場\(\boldsymbol E\)と磁場\(\boldsymbol B\)を代入して計算していきます。
$$\frac{\partial B_{x}(x,t)}{\partial t}=0 \tag{19 – 1}$$
$$-\frac{\partial E_{z}(x,t)}{\partial x}+\frac{\partial B_{y}(x,t)}{\partial t}=0 \tag{19 – 2}$$
$$\frac{\partial E_{y}(x,t)}{\partial x}+\frac{\partial B_{z}(x,t)}{\partial t}=0 \tag{19 – 3}$$
マクスウェル方程式の式(3)を変形した次式
$$\mathrm{rot}{\boldsymbol{B}}-c_0\frac{\partial \boldsymbol{E}}{\partial t}=0 \tag{20}$$
について先程と同様に計算します。
$$-c_0\frac{\partial E_{x}(x,t)}{\partial t}=0 \tag{21 – 1}$$
$$-\frac{\partial B_{z}(x,t)}{\partial x}-c_0\frac{\partial E_{y}(x,t)}{\partial t}=0 \tag{21 – 2}$$
$$\frac{\partial B_{y}(x,t)}{\partial x}-c_0\frac{\partial E_{z}(x,t)}{\partial t}=0 \tag{21 – 3}$$
式(1)と式(21-1)より
$$\mathrm{div}{\boldsymbol{E}}=\frac{\partial E_{x}(x,t)}{\partial t}=0$$
$$\frac{\partial E_{x}(x,t)}{\partial x}=\frac{\partial E_{x}(x,t)}{\partial t}=0 \tag{22}$$
また、式(2)と式(19-1)より
$$\mathrm{div}{\boldsymbol{B}}=\frac{\partial B_{x}(x,t)}{\partial t}=0$$
$$\frac{\partial B_{x}(x,t)}{\partial x}=\frac{\partial B_{x}(x,t)}{\partial t}=0 \tag{23}$$
これらを\(x\)と\(t\)についてそれぞれ積分しても定数となります。ここでは定数を0とします。以上より次式が得られます。
$$E_{x}(x,t)=B_{x}(x,t)=0 \tag{24}$$
式(24)より、\(x\)軸方向に対してのみ値が変化する場合電場と磁場は\(x\)成分を持たないことになります。電場と磁場は\(yz\)平面内を向いていることになります。ここで、考えやすくするために電場が\(y\)成分のみ持つとします。つまり電場の\(z\)成分は0になります。
$$E_{z}(x,t)=0 \tag{25}$$
これを式(19 – 2)、(21 – 3)に代入すると
$$\frac{\partial B_{y}(x,t)}{\partial t}=\frac{\partial B_{y}(x,t)}{\partial x}=0 \tag{26}$$
よって
$$B_{y}(x,t)=0 \tag{27}$$
磁場の\(y\)成分は0で\(z\)成分のみが残り、電場は磁場と垂直な成分を持つことになります。これを表したのが図1です。電場と磁場は進行方向に対して右ねじの法則となるような関係になっています。

図1
次に式(19-3)の第二項を移項して両辺を\(x\)で偏微分し、式(21-2)を代入します。
$$\frac{\partial^2 E_{y}(x,t)}{\partial x^2}=-\frac{\partial}{\partial t}\frac{\partial B_{z}(x,t)}{\partial x}$$
$$\frac{\partial^2 E_{y}}{\partial t^2}=\frac{1}{c_0}\frac{\partial^2 E_{y}(x,t)}{\partial x^2} \tag{28}$$
同様に式(21-2)を\(x\)で偏微分し、式(19-3)を代入します。
$$\frac{\partial^2 B_{z}(x,t)}{\partial x^2}=-c_0\frac{\partial}{\partial t}\frac{\partial E_{y}(x,t)}{\partial x}$$
$$\frac{\partial^2 B_{z}}{\partial t^2}=\frac{1}{c_0}\frac{\partial^2 B_{z}(x,t)}{\partial x^2} \tag{29}$$
これらは式(14)の形の1次元の波動方程式と一致しています。この2つの式の関係について見ていきます。式(25)より電場は\(y\)成分を持たないので\(z\)成分を次のように定義します。
$$\begin{align}E_y(x,t)&=X\mathrm{sin}2\pi(\frac{x}{\lambda}-\frac{t}{T}) \\
&=X\mathrm{sin}\frac{2\pi}{T}(\frac{x}{c_0}-t) \tag{30} \end{align}$$
ここでTは周期、\(\lambda\)は波長を表し位相速度\(c_0\)との次の関係を利用しました。
$$\lambda=c_0T \tag{31}$$
式(31)を電磁波の導出に利用した式(19-3)に代入します。
$$\frac{\partial E_{y}(x,t)}{\partial x}=\frac{2\pi}{c_0T}X\mathrm{cos}\frac{2\pi}{T}(\frac{x}{c_0}-t)=-\frac{\partial B_{z}(x,t)}{\partial t} \tag{32}$$
\(t\)で積分して
$$B_{z}(x,t)=\frac{1}{c_0}\mathrm{sin}\frac{2\pi}{T}(\frac{x}{c_0}-t) \tag{33}$$
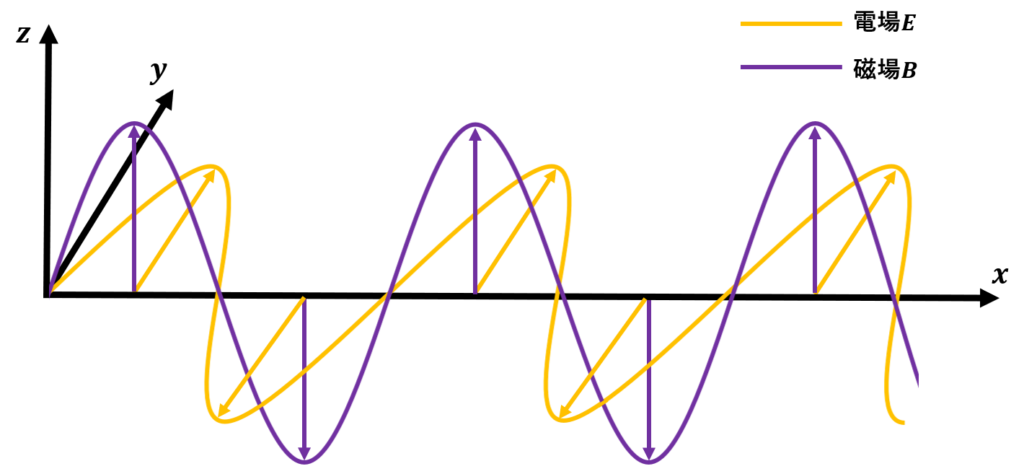
図2
式(30),(33)より、電場と磁場は成分は互いに垂直で振幅が異なる同じ周波数の波で伝わることになります。これを表したのが図2にです。このように電磁波は電場と磁場が同じように伝わっていくことになります。
4.特殊相対性理論へ繋がる
相対性理論はアインシュタインが提案したことで有名ですが、特殊相対性理論は電磁気学と強い関わりがあります。特殊相対性理論ではローレンツ変換という座標変換を行いますが、アインシュタインではなくローレンツの名前からとられています。特殊相対性理論は光速がどの座標系から見ても一定であるということが前提となっていて、アインシュタインが提案したアプローチは電磁気学とは異なる方法です。電磁波の波動方程式に出てくる位相速度についてはどの座標から見た速度なのかが議論になり、どの座標系から見ても位相速度が一定となるように座標変換をするとアインシュタインが導いたものと同じ式(ローレンツ変換)が導かれます。今後の記事では特殊相対性理論についてもまとめていきたいと思います。
今回の記事は以上になります。
参考文献
1.電磁気学、砂川重信
2.波動方程式の解き方、須藤彰三
3.趣味で物理学、広江克彦


コメント